| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- springboot
- Spring
- 냄새와 휴리스틱
- 코딩테스트
- DxTrace
- BOJ
- 가장 긴 증가하는 부분 수열2
- 자바의 정석
- 11758번
- 11286번
- 1300번
- 2206번
- 17장
- programmers
- Adapater Pattern
- 프로그래머스
- java
- Dxerr.h
- 코딩 테스트
- 백준
- 9장
- 2166번
- 클린코드
- Design Pattern
- 1043번
- SerialDate 리펙터링
- Design Patterns
- 2156번
- 10830번
- java의 정석
- Today
- Total
Don't give up!
[프로그래머스] 멀쩡한 사각형 (java) 본문
코딩테스트 연습 - 멀쩡한 사각형 | 프로그래머스 (programmers.co.kr)
코딩테스트 연습 - 멀쩡한 사각형
가로 길이가 Wcm, 세로 길이가 Hcm인 직사각형 종이가 있습니다. 종이에는 가로, 세로 방향과 평행하게 격자 형태로 선이 그어져 있으며, 모든 격자칸은 1cm x 1cm 크기입니다. 이 종이를 격자 선을
programmers.co.kr
어떻게 생각하고 문제를 풀었는가?

시작점 (0,0), 도착점 (h,w)인 직선은 (1,w/h), (2,2w/h)인 점을 지나갑니다.
직선의 기울기가 일정하므로 직선이 지나는 사각형의 패턴은 y값이 정수가 정수로만 이루어진 점들 사이의 구간의 패턴으로 볼 수 있습니다.
따라서 (0,0)부터 정수 (x,y)까지의 범위에서 직선이 지나는 사각형의 수 X 패턴의 수를 계산하여 전체 범위에서 직선이 지나는 사각형의 수를 구할 수 있습니다.
코드
class Solution {
public long solution(int w, int h) {
int x=0,y=0;
long across=0L;
for(x=1; x<=h; x++){
double ny = (double)x*w/h;
across += Math.ceil(ny) - y;
if(ny - (int)ny == 0.f) break;
y = (int)Math.floor(ny);
}
return (long)w*h - across * (h/x);
}
}x=1부터 직선의 y값이 정수가 될때까지 반복하며 지나는 사각형의 수를 계산하는 코드를 작성하였습니다.
Math의 ceil과 floor 함수를 사용하여 사각형의 수를 계산하였습니다.
예를 들어 (1, 2/3), (2, 4/3)을 지나는 직선은 y=0과 y=1, y=1과 y=2사이의 사각형 2개를 지나가므로 2-0=2로서 계산할 수 있습니다.
정밀도
import java.lang.Math;
class Solution {
public long solution(int w, int h) {
int x=0,y=0;
long across=0L;
double angle = (double)w/h;
for(x=1; x<=h; x++){
double ny = x*angle;
across += Math.ceil(ny) - y;
if(ny - (int)ny == 0.f) break;
y = (int)Math.floor(ny);
}
return (long)w*h - across * (h/x);
}
} 기울기를 변수로 이용하여 실행해보았지만 정답이 되지 못하였습니다.
이는 double에 저장할 수 있는 값의 범위를 넘어섰기 때문입니다.
실수를 저장하는 float과 double은 소수부분을 표현하기 위해 부동소수점을 사용합니다.
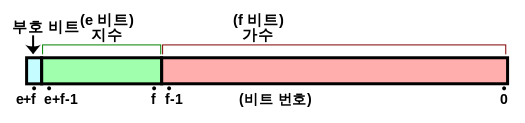
float타입은 4byte 크기 실수형 타입으로 지수를 8bit 사용합니다. 지수의 1bit를 부호를 위한 bit로 두었을 때 최대 지수값은 2^7 입니다. 남은 23bit는 가수를 위해 사용되고 1.xxx X 2^n로 표현되는 xxx 값을 가수로 저장합니다.
2^(-23)은 0.0000001192(약 10^-7)이므로 소수점 이하 6자리까지만 float에 저장될 수 있습니다.
이것이 'float 타입의 정밀도는 7자리다'라고 표현하는 이유입니다.
double 타입은 지수를 16bit로 늘렸으므로 정밀도가 15자리입니다.
1억이하의 자연수를 갖는 입력 값 w와 h는 최대 값이 10^8로 float과 double 모두 최대 값을 표현할 수 있지만 w=10, h=3과 같이 w/h의 연산 결과가 소수점 이하 15자리를 넘어가는 경우 두 코드는 다음과 같이 결과가 달라질 수 있습니다.
1. double 자료형에 w/h를 먼저 저장한 후 x*(w/h)를 수행한 경우
3.33333333333333이 변수로 저장됨
x=10일때 y값은 33.33333333333330
2. x*w/h을 double 자료형에 저장할 경우
x=10일때 x*w=100, y=100/3 = 33.33333333333333
나눗기 연산을 사용하고, 결과를 실수형 타입에 저장하고자 할때 정밀도를 고려해야함을 확인하였습니다.
'Coding Test > Programmers' 카테고리의 다른 글
| [프로그래머스] 조이스틱 (java) (2) | 2021.05.11 |
|---|---|
| [프로그래머스] 게임 맵 최단거리 (java) (0) | 2021.05.08 |
| [프로그래머스] H-Index(java) (0) | 2021.05.07 |
